Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Bongsuk Kwon
Optimal Experimental Design for Uncertain Systems Based on Coupled Differential Equations
Jul 12, 2020Figures and Tables: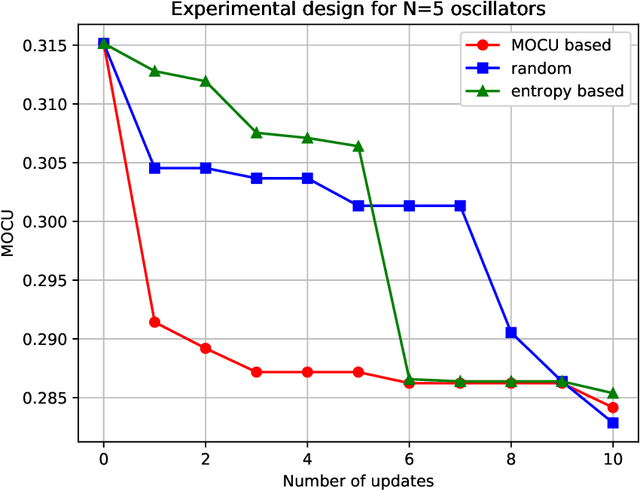
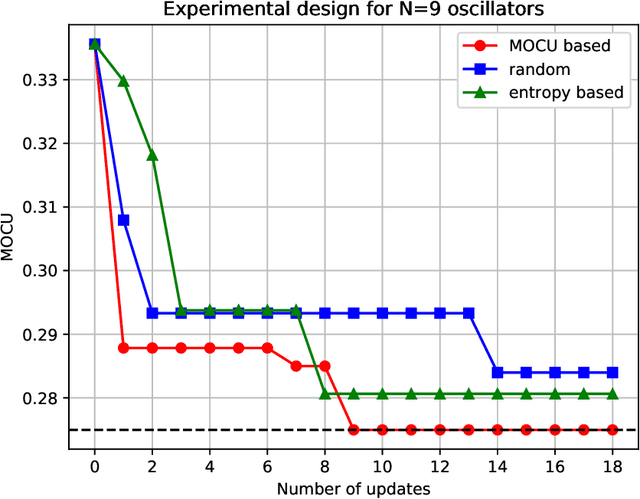


Abstract:We consider the optimal experimental design problem for an uncertain Kuramoto model, which consists of N interacting oscillators described by coupled ordinary differential equations. The objective is to design experiments that can effectively reduce the uncertainty present in the coupling strengths between the oscillators, thereby minimizing the cost of robust control of the uncertain Kuramoto model. We demonstrate the importance of quantifying the operational impact of the potential experiments in designing optimal experiments.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge